揭秘数学界的璀璨明珠——欧拉的函数

亲爱的读者，你是否曾在数学的海洋中迷失方向，被那些复杂的公式和定理搞得头昏脑胀？今天，就让我们一起揭开数学界璀璨明珠——欧拉的函数的神秘面纱，探索它那令人着迷的数学世界。

一、欧拉的函数：数学界的“万能钥匙”

欧拉的函数，又称欧拉商数，是数学中一种特殊的数论函数。它由18世纪伟大的数学家莱昂哈德·欧拉定义，被誉为“数学界的万能钥匙”。这个函数在数学的各个领域都有着广泛的应用，从物理学到密码学，从数论到组合数学，都离不开它的身影。

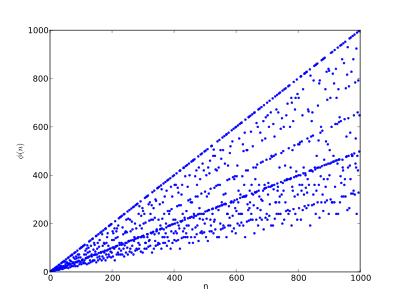
二、欧拉的函数：定义与性质

欧拉的函数（记作φ(n)）表示小于或等于正整数n的所有正整数中，与n互质的数的个数。所谓互质，指的是两个数的最大公约数为1。例如，φ(8) = 4，因为小于或等于8的正整数中，与8互质的数有1、3、5、7，共4个。

欧拉的函数具有以下性质：

1. 对于任意正整数n，φ(n) ≥ 1。

2. 如果n是质数，则φ(n) = n - 1。

3. 如果n是合数，则φ(n)可以分解为n的所有质因数的欧拉函数值的乘积。

4. 如果m和n是两个互质的正整数，则φ(mn) = φ(m)φ(n)。

这些性质使得欧拉的函数在数学研究中具有极高的价值。

三、欧拉的函数：应用与实例

欧拉的函数在数学的各个领域都有着广泛的应用，以下列举几个实例：

1. 物理学：欧拉的函数在物理学中可以用来描述物理系统的对称性。例如，在量子力学中，欧拉的函数可以用来描述粒子的自旋。

2. 密码学：欧拉的函数在密码学中有着重要的应用。例如，在RSA加密算法中，欧拉的函数被用来计算公钥和私钥的模逆元。

3. 数论：欧拉的函数在数论中有着广泛的应用。例如，它可以用来证明费马小定理和欧拉定理等。

4. 组合数学：欧拉的函数在组合数学中可以用来计算有限域上多项式的根的个数。

四、欧拉的函数：数学巨匠的智慧结晶

欧拉的函数是数学巨匠莱昂哈德·欧拉的智慧结晶。他不仅在数学领域有着卓越的成就，还在物理学、力学、图论等多个领域都有着重要的贡献。欧拉的函数只是他众多成就中的一颗璀璨明珠。

五、

欧拉的函数是数学界的一颗璀璨明珠，它那神秘而迷人的数学世界令人着迷。通过本文的介绍，相信你已经对欧拉的函数有了更深入的了解。在今后的数学探索中，让我们继续追寻欧拉的足迹，感受数学的魅力。